Terms and Conditions – A Fine-Tuned Critique of Ikeda and Jefferys (Part 1)

What do you know? – A Fine-Tuned Critique of Ikeda and Jefferys (Part 2) »

Terms and Conditions – A Fine-Tuned Critique of Ikeda and Jefferys (Part 1)

October 26, 2010 by lukebarnes

Once more unto the breach, dear friends. (Another long fine-tuning post, I’m afraid …)

An oft-cited article on the fine-tuning of the universe for intelligent life was written by Michael Ikeda and Bill Jefferys, and goes by the title: “”The Anthropic Principle Does Not Support Supernaturalism”. It appears online here, and ~~to the best of my knowledge has not been published anywhere~~ has been published in “The Improbability of God“, edited by Michael Martin and Ricki Monnier (edit: 3/11/2010).

IJ’s Argument

Unless otherwise noted, quotes are from Ikeda and Jefferys (hereafter IJ). Their central argument is as follows. Let:

L = The universe exists and contains Life.
F = The conditions in the universe are ‘life-Friendly,’ that is, the conditions in our universe permit or are compatible with life existing naturalistically.
N = “The universe is governed solely by Naturalistic law.” The negation, ~N, is that it is not governed solely by naturalistic law, that is, some non-naturalistic (supernaturalistic) principle or entity is involved. N and ~N are not assumptions; they are hypotheses to be tested.

L is, of course, true of our universe. For the sake of argument, IJ assume that F is true. N and ~N are taken to have an a priori non-zero probability of being true. Now, the anthropic principle roughly states that living observers must observe conditions that permit the existence of observers. IJ formulate this as:

$P(F|N\&L) = 1$ . (1)

N appears in the expression just in case a supernatural agent decides to miraculously sustain life in a non-life-friendly universe.

Now, after dealing with the fallacious¹ argument $P(F|N) \ll 1 \Rightarrow P(N|F) \ll 1$ , IJ reach their Bayesian climax:

$P(N|F\&L) = \frac{P(F|N\&L) P(N|L)} {P(F|L)}$ (Bayes Theorem)
$= \frac{P(N|L)} {P(F|L)}$ (using 1)
$\ge P(N|L)$ (since $P(F|L) \le 1$ )

Thus, the fine-tuning of the universe for intelligent life is at best irrelevant to the truth of naturalism, and could actually make it more likely. The fine-tuning of the universe, even if it is true, cannot support supernaturalism. Notice that all probabilities are conditioned on L. As IJ say:

… for an inference to be valid, it is necessary to take into account all known information that may be relevant to the conclusion. In the present case, we happen to know that life exists in our universe (i.e., that L is true). Therefore, it is invalid to make inferences about N if we fail to take into account the fact that L, as well as F, are already known to be true. It follows that any inferences about N must be conditioned upon both F and L … In inferring the probability that N is true, it is entirely irrelevant whether P(F|N) is large or small. It is entirely irrelevant whether the universe is “fine-tuned” or not. Only probabilities conditioned upon L are relevant to our inquiry.

I have two responses. Here I will contend that IJ’s formulation of the argument is incomplete. In the second part, I’ll raise a few issues with this “conditioning on everything” idea.

My Formulation

Here is how I would (roughly) formulate the argument from fine-tuning. Let the “physics” of a universe refer to its laws + initial conditions + physical constants. Let a “universe” be a connected region of spacetime over which physics is effectively constant². We consider life to be a class of physical phenomena – we won’t need a precise definition. I will drop the ampersand in my notation, i.e. $AB \equiv A\&B$ , and $Latex$ typesetting will distinguish my premises from IJ’s. Let:

$L$ = this universe contains life
$X$ = the physics of this universe includes conditions sufficient for the eXistence of life
$E$ = the physics of this universe includes conditions sufficient for the evolution of life
$N$ = the natural phenomena of this universe are the causal products of the physics of this universe. (Remember that “physics” includes initial conditions in my terminology.)
$I ~ (I_E)$ = the causes that established the physics of this universe were indifferent to whether our particular physics would allow the survival (evolution) of life.
$F ~ (F_E)$ = in the set of possible physics, the subset that permit the existence (evolution) of life is very small. In other words, the physics of a particular universe must be fine-tuned if that universe is to support the existence (evolution) of life. (I won’t be too worried by the difference between $F,~I$ and $F_E,~I_E$ here.)

The anthropic principle then states: $P(X|LN) = 1$ . (2)

A few words on the difference between my formulation and IJ’s.

The difference between $X$ and $E$ is clears up a misconception in IJ. They argue that intelligent design advocates simultaneously affirm that the universe is and is not “life-friendly” – Ross says that the universe is so life-friendly that God must have set it up, while Behe says that the universe is not life-friendly so God must have created life supernaturally. But this is simply confused. Ross argues from $X$ and $F$ , Behe from $\overline{E}$ (“not-E”). In other words, Ross is saying that it’s a miracle to have a stable planet orbiting a stable star in a long-lived universe stocked with atoms that are able to form complex structures. Behe, on the other hand, argues that these conditions are not sufficient to produce all the complexities of life as we know it. Ross and Behe may be mistaken, but they are not contradicting each other.
IJ’s “N” slightly misses the point. The question is whether physics is fine-tuned and what we can conclude from this, not whether there are any exceptions to the laws of nature³. A deist could affirm that “the universe is governed by naturalistic laws”, and still conclude that fine-tuning is evidence of a cosmic designer of those laws. As a result, the fine-tuning of the universe is a test of the hypothesis $I$ , rather than $N$ .
The important observation in the context of this argument is $F$ not $X$ . The claim that the universe is fine-tuned for intelligent life is more than a claim about this universe. It is a counterfactual claim about how things could have turned out. $X$ is almost certainly true – it follows almost inevitably from $L$ , which is true. $F$ , however, does not follow from $L$ .

We can now formulate IJ’s argument in my terminology.

$P(N|XL) = \frac{P(X|NL) P(N|L)} {P(X|L)}$ (Bayes Theorem)
$= \frac{P(N|L)} {P(X|L)}$ (using 2)
$\ge P(N|L)$ (since $P(X|L) \le 1$ )

This shows that, given that life exists in this universe, the fact that the physics of this universe includes conditions sufficient for the existence of life makes it not less likely that the continued existence of life is within the causal powers of the physics of this universe. That was a horrendous sentence. In short, life exists. We then learn that physics of the universe is capable of sustaining life. This possibly makes it more likely that life is sustained purely by physical means, without supernatural intervention.

This is all fine, but it has nothing to do with fine-tuning. At best, it could show that the hypothesis that angels push the planets around in their orbits becomes less likely once we learn that Newton’s laws of motion and gravitation can do the job. (Though, as Richard Feynman pointed out, perhaps Newton only showed that the angels push radially rather than tangentially.) It says nothing about what we can conclude from the fact that, if the universe were not three-dimensional, Newtonian gravity would produce unstable planetary orbits.

What we really want to know is the ratio:

$R \equiv \frac{P(I|LXFN)} {P(\overline{I}|LXFN)} = \frac{P(X|ILFN)} {P(X|\overline{I}LFN)} \frac{P(I|LFN)} {P(\overline{I}|LFN)}$ (3)

Note that we are conditioning on $N$ – it is one of the strengths of the argument that we are not appealing to supposed phenomena that are beyond the powers of physical laws.

What effect does the anthropic principle (2) have on $R$ ? Using the general principle: $P(A|B) = 1 \Rightarrow P(A|BC) = 1$ for any $C$ such that $P(C|B) \neq 0$ , it follows from (2) that:

$P(X|LN) = 1 ~ \Rightarrow ~ P(X|ILFN) = P(X|\overline{I}LFN) = 1$

Thus, (3) becomes (using Bayes theorem again):

$R = \frac{P(I|LFN)} {P(\overline{I}|LFN)} = \frac{P(L|IFN)} {P(L|\overline{I}FN)} \frac{P(I|FN)} {P(\overline{I}|N)}$

Further, if the life-permitting region of possible-physics-space is small, then it is small independently of whether the physics of our universe is effected indifferently or not. Thus, $P(F|IN) = P(F|\overline{I}N)$ , which implies:

$\frac{P(I|FN)} {P(\overline{I}|FN)} = \frac{P(I|N)} {P(\overline{I}|N)}$

Putting all together gives:

$\frac{P(I|LXFN)} {P(\overline{I}|LXFN)} = \frac{P(L|IFN)} {P(L|\overline{I}FN)} \frac{P(I|N)} {P(\overline{I}|N)}$

Then, we argue as follows:
i) Because the life-permitting subset is very small, an indifferent physics-producing process is very unlikely to hit upon a life-permitting universe. This would include simply positing physics as a brute fact. Thus, $P(L|IFN) \ll 1$ . (As IJ tell us, $P(L|IFN)$ is generally not equal to 1, even if we have observed that $L$ is true).
ii) There are possible hypotheses under which the physics of this universe is effected with “life in mind”. For the union of all such hypotheses (i.e. $\overline{I}$ ), $P(L|\overline{I}FN)$ is not small.
iii) Thus, $P(L|IFN) \ll P(L|\overline{I}FN)$ .
iv) Thus $\frac{P(I|LXFN)} {P(\overline{I}|LXFN)} \ll \frac{P(I|N)} {P(\overline{I}|N)}$

We conclude that learning $F$ has increased the probability that whatever set in place the physics of our universe was not indifferent to whether our universe could support life.

Caveats

None of this proves that $\overline{I}$ is true:

We could still conclude that $P(\overline{I}|N)$ is very small or inscrutable, derailing the argument.
The argument above assumes that this universe is the only universe. As IJ note (and I agree), $F$ can also be taken as evidence for a multiverse.
There are non-supernatural hypotheses consistent with $\overline{I}$ . In “At Home in the Universe” (and elsewhere), John Wheeler argued for the participatory anthropic principle – from the centrality of observership to quantum mechanics (“no elementary phenomenon is a phenomenon until it is a registered phenomenon”), Wheeler proposes that the universe is like a self-excited circuit: “beginning with the big bang, the universe expands and cools. After eons of dynamic development it gives rise to observership. Acts of observer-participancy … in turn give tangible “reality” to the universe not only now but back to the beginning”. The laws of nature are “higgledy-piggledy [built] out of the statistics of billions upon billions of acts of observer-participancy”. Paul Davies favours similar ideas in “The Goldilocks Enigma”. These are admittedly very unorthodox ideas, but they do show that $\overline{I}$ is broader than theism …
Philosophical arguments from fine-tuning to the existence of God (usually) recognise that $\overline{I}$ is not enough. For example, Swinburne argues that intelligent, moral agents are a kind of entity that God would want to create. Collins has a similar discussion, arguing that at the very least, the conjunction $I$ + “only this universe exists” is strongly disfavoured by the fine-tuning of the universe, leaving the atheist (almost all of whom affirm $I$ ) needing to produce independent reasons for believing that a life-permitting multiverse exists.
Of course, $F$ could turn out to be false or unknowable.

Note that running the entire argument through assuming $E$ instead of $X$ doesn’t change much. Equation (3) still holds with this replacement. If anything, the region of possible-physics-space that allows the evolution of life is even smaller than the region that merely allows the existence of life, strengthening our conclusion.

In conclusion, it is possible that the fine-tuning of the universe supports some type of supernaturalism, contrary to the claim of IJ that it is impossible. Whether it actually does is a question for another day. In part 2, I’ll raise a few queries about IJ’s insistence that we condition on everything we know.

_____________________________________

1. Which might be a straw man – they don’t cite anyone who actually makes this error, and I’m not aware of any such case. In fact, they don’t cite any of the fine-tuning literature except for Hugh Ross.

2. Footnote: we may wish to stipulate that any observer observes only one universe by definition. These finer points will not effect our discussion.

3. It is possible (i.e. I’m still thinking it through) that the sentence, “a sufficiently powerful supernatural principle or entity (deity) could sustain life in a universe with laws that are not “life-friendly”, simply by virtue of that entity’s will and power” is self-contradictory. In a theistic universe, the laws of nature simply are the way that God runs and sustains the universe. The laws of nature themselves exist “by virtue of that entity’s will and power”. God logically cannot make a consistent exception to the laws of nature – the exception would become the rule. (This doesn’t a priori rule out singular exceptions i.e. miracles). It follows that we don’t need $N$ to appear in the anthropic principle i.e. $P(X|LN) = P(X|L) = 1$ .

More of my posts on fine-tuning are here.

About these ads

Posted in Astronomy, fine tuning, Science, Science and the Public, The Universe | Tagged anthropic, fine tuning, ikeda, Jefferys | 29 Comments

29 Responses

on October 26, 2010 at 10:47 pm | Reply rickryals

How does the anthropic statement change if ‘the causes that established the physics of this universe’… require life as a function of the thermodynamics, like an energy conservation law that correlates life to the structure mechanism in the form of a cosmological principle that resolves the problem definitively, from theoretically expected first principles, rather than cop-outs, like probabilities and god?
- on January 5, 2013 at 4:03 am | Reply James
  
  Of course the Anthropic principle does support it. neither does Multiverse. But what these biased thinkers dont seem to comprehend is that everyone with a rational mind knows that these ad hoc hypothesis are directly confirming they have been thoroughly beaten,
  
  They tried to show the world only “looks” designed and they found the math and equations are WORSE than what we see. They must be designed.
  
  Its over. Its done. You have 2 choices…The Obvious–Design–of which the majority of all humans that have ever lived can see in all of 3 seconds. Or Multi universe maker machine that makes everything possible. We are simply not open to any other option.
  
  The very fact that these atheists entered the field of origins to confirm their world view( 75% of Doctors are theists showing those with aptitudes in science branch off according to worldview) have now retreated to multiverse have clearly and pathologically confirmed their view is based on BIAS.
  
  They are the only ones who haven’t got the memo that they are defeated
  - on January 5, 2013 at 3:45 pm rickryals
    
    I’m not exactly sure what you’re saying James, as I said nothing about ID and that isn’t the most probable explanation for our existence even if we aren’t here by accident. I agree with you point about bias though, as it is dead on the money.
    
    Regardless, I have a lot more respect for Luke than I did almost four years ago when I wrote my comments, because anybody that puts a formal beat-down on denialists like Vic Stenger is all right in my book, and Luke has done just that since this article was published.
on October 27, 2010 at 2:47 pm | Reply lukebarnes

I don’t understand the question …

* What is “the anthropic statement”?
* How can something be “a function of thermodynamics”?
* What do you refer to when you say “an energy conservation law that correlates life to the structure mechanism in the form of a cosmological principle”?
* What “theoretically expected first principles”?
* How are “probabilities” a cop-out?
on October 27, 2010 at 3:22 pm | Reply rickryals

You said that your formulation derives that:
The anthropic principle then states: P(X|LN)=1

Where I(I_E) = the causes that established the physics of this universe were indifferent to whether our particular physics would allow the survival (evolution) of life.

So I asked what the principle would state if the universe, (not god), is NOT indifferent…

But the fact that you don’t already know the answer to your last two questions speaks volumes about what you know, rather, don’t know about physics, so maybe I’m just wasting my time..
on October 27, 2010 at 6:04 pm | Reply lukebarnes

The anthropic principle would state exactly the same thing. Observers must observe conditions that permit the existence of observers. It’s a selection effect. It’s not an observation, or a physical principle, or an ideological principle. A good analogy is Malmquist bias in astrophysics – we only ever observe objects that are bright enough to be detectable. It’s obviously true but sometimes easily overlooked.

* What “first principles” are you talking about? Mathematical axioms? Quantum Field Theory? General Relativity? String theory? M-theory? Loop quantum Gravity? Twistor theory? The laws of thermodynamics? Newton’s laws? Quantum mechanics? Spacetime symmetries and Noether’s theorem? Supersymmetry? The holographic principle? The cosmological principle? Or some other theory you’ve devised perhaps?

* the probability of a fair coin coming up tails when flipped is 0.5. Is that a cop-out? Or are you talking about quantum probabilities? Or are you not a fan of Bayes theorem? Or is all of probability theory fundamentally flawed in some way?

In short, what are you talking about? You might also want to explain how you take a request for clarity to be incontrovertible evidence for lack of knowledge of physics …
on October 27, 2010 at 8:00 pm | Reply rickryals

“THE” anthropic principle, huh? I hate to tell you, but one lame variant interpretation isn’t “THE” anthropic principle, and the weak interpretation doesn’t even apply unless you assume that there is a multiverse because the OBSERVATION is not the least bit weak.

Pretty much everyone who knows anything about physics knows that the most natural expectation is for the apparent fine-tuning of the universe is a cosmological structure principle that explains from first principles why the universe is configured in the otherwise completely unexpected manner that we find it in. The multiverse and selection effects are one plausible yet unjustified solution to the problem, but as David Gross says, that the failure of physicists to produce said true dynamical principle is the single biggest failure of scientists in the last 50 years.
on November 3, 2010 at 9:38 pm | Reply shitikov_yury

Thank’s a lot! I feeled that Ikeda and Jefferys omitted some important points in theit theorem (exactly like dog – feeled but coudn’t express in words)))))
on November 5, 2010 at 8:31 am | Reply What do you know? – A Fine-Tuned Critique of Ikeda and Jefferys (Part 2) « Letters to Nature

[...] is my second critique of the work of Ikeda and Jefferys (IJ) on the fine-tuning of the universe for intelligent life. IJ [...]
on December 2, 2010 at 1:46 am | Reply Donald

This is cool. I came up with what I think is a similar set of arguments against Ikeda/Jefferys a year or two ago, but didn’t know who to email about it. I mention part of my argument in the comments section at problogion here–

link

I have to look more closely at your argument and go back and look at mine, but this part of yours–

“In short, life exists. We then learn that physics of the universe is capable of sustaining life. This possibly makes it more likely that life is sustained purely by physical means, without supernatural intervention.

This is all fine, but it has nothing to do with fine-tuning”

sounds just like what I had concluded about Jefferys/Ikeda.
on January 17, 2011 at 5:41 pm | Reply Greg Fish

With all due respect, all this math seems like much ado about things we’re trying to make artificially complex. Bayesian statistics imply that we have evidence of what we’re trying to prove but when it comes to binary statements such as “the universe has life” and “the laws of physics allow for life”, we’re basically dealing with either a P of 0 or a P of 1.

The question of whether the universe is fine-tuned for life or not depends on the life in question. If we have methane-breathing sentient life which would most likely exist in the temperature range of -250 °F and -350 °F or so and had some form of conscious thought, it would conclude that the universe was fine-tuned for it because it exists and the conditions are so friendly for it while we, who breather a mix of oxygen and nitrogen and survive best in the 30 °F to 100 °F temperature range would think that the conditions specified previously are completely hostile to all living things.

We only know that life in this universe does exist and without taking into account any potential alien life out there or noting that if the universe evolved different it may have different types of life than exist in the current universe, we can’t even pretend that the universe is fine tuned for life.
on July 19, 2011 at 5:27 am | Reply ID Foundations, 6: Introducing* the cosmological design inference | Uncommon Descent

[...] More technical response to Ikeda and Jeffreys’ Bayesian probability critique: 1, 2. (DM, kindly take notice. This critique, by reasonable extension, also applies to [...]
on January 27, 2012 at 9:59 pm | Reply Brent Meeker

The argument of IJ is much simpler than you make it. Their argument is against a theist god, not a deist one. A theist god could sustain life in an unfriendly universe. This does not imply some consistent physics to support them or a one-time exception. A theist god could populate the universe with, for example, angels that needed no external energy source. Humans, or life in general, could exist with some separate ‘miraculous’ physics, different from inanimate matter – and in fact that was the common assumption in earlier times. Such miraculous existence would certainly be evidence for a theist god, one who is not indifferent to human life. Then it is simple probability logic that the contrary cannot count as evidence for the theist god. But the contrary, that human life exists naturally, is exactly what we observe.
on February 5, 2012 at 2:31 am | Reply lukebarnes

I said that in my post: “the fact that the physics of this universe includes conditions sufficient for the existence of life makes it not less likely that the continued existence of life is within the causal powers of the physics of this universe. … it could show that the hypothesis that angels push the planets around in their orbits becomes less likely once we learn that Newton’s laws of motion and gravitation can do the job.”

If that is their argument, then that’s fine. It just has nothing whatsoever to do with fine-tuning.

See footnote 3 above for my preliminary thoughts about their argument.
on June 11, 2012 at 12:53 pm | Reply Wolfbone

Thanks for the invitation in your Guardian comment (link ^^^).

I didn’t say your calculation was wrong – strictly speaking it isn’t – I said your critique was wrong. You claim to be doing an inference calculation for the probability of (hypothesis) ‘I’ on learning (data) ‘F’ but you’re not. The elementary ‘Bayesian’ likelihood ratio test which you’re (quite rightly) using for your calculation has the correct form, but that just makes it all the more easy to see that the data being used to update the probability of hypothesis ‘I’ isn’t ‘F’! In (3) it is ‘X’ (on background ‘LFN’) and further down it is ‘L’ (on background ‘FN’). Your conclusion¹ is a non sequitur.

¹ “ We conclude that learning ['F'] has increased the probability that whatever set in place the physics of our universe was not indifferent to whether our universe could support life.”
on June 11, 2012 at 11:13 pm | Reply lukebarnes

The calculation is of the probability of $I$ given multiple pieces of evidence, $L$ , $X$ , $F$ , and $N$ . We want to calculate:

$R = \frac{p(I|LXFN)}{p(\bar{I}|LXFN)}$

Whenever we condition on multiple pieces of information, we have a choice about how to evaluate the expression above. Given Bayes theorem, we can pull this equation apart in a number of different ways. The following are mathematically equivalent:

$R = \frac{p(X|ILFN)p(L|IFN)p(F|IN)p(I|N)}{p(X|\bar{I}LFN)p(L|\bar{I}FN)p(F|\bar{I}N)p(\bar{I}|N)}$
$= \frac{p(F|ILXN)p(L|IXN)p(X|IN)p(I|N)}{p(F|\bar{I}LXN)p(L|\bar{I}XN)p(X|\bar{I}N)p(\bar{I}|N)}$

These are mathematically equivalent. The choice between them is not a choice of what information is updating what hypothesis. Which one of these we use to calculate R is dependent on which of these terms we can actually calculate. Given the anthropic principle and $p(F|IN) = p(F|\bar{I}N)$ (as argued above), we should use the first form, as I did in my post, as more simplification is possible. We can’t use the anthropic principle to simplify the second one.

So, if

a) R is the right quantity to focus our attention (which I think you agree with).
b) I have correctly derived that
$R = \frac{p(L|IFN)p(I|N)}{p(L|\bar{I}FN)p(\bar{I}|N)}$ . (I think you agree)
c) My conclusions i) to iv) follow from this expression,

then my conclusions are watertight. No logical inconsistency or non-sequitur can sneak in if I ask the right question (R) and the laws of probability are followed.

On the other hand, the argument of Ikeda and Jeffreys obviously fails, since they don’t even take into account the fine-tuning of the universe for intelligent life. They only take into account the fact that our universe is life-friendly, not that life-friendliness is rare in the set of all possible universes.
on June 12, 2012 at 8:00 pm | Reply Wolfbone

“The calculation is of the probability of ['I'] given multiple pieces of evidence [...]”

This is all very perplexing. Your setup of (3) seems to indicate that you’re well aware that it’s impossible to calculate the actual probability of ‘I’ or the posterior odds ratio ‘R’ of ‘I’ against ‘~I’, and that all we can do is construct a (semi-quantitative) likelihood ratio from specified facts/data and see how it changes the prior odds ratio. Encouragingly, you also explicitly state that “The important observation [facts/data] in the context of this argument is [F]”, and at first it does look like you’re going to do the appropriate ‘Bayesian’ inference: first transforming (3) – which is clearly a (formally) correct ‘Bayesian’ inference on ‘X’ – into a correct (and informative) inference on ‘F’. But instead you transform it into a (formally) correct inference on ‘L’¹ and conclude (as I quoted last time) that the result of this inference on ‘L’ is the result of an inference on ‘F’!

“No logical inconsistency or non-sequitur can sneak in if I ask the right question (R) and the laws of probability are followed.”

But “[what is] (R)?” is /not/ the right question, and while you’ve followed some of the laws of probability in your calculations, you’ve disregarded the ones of particular relevance here: the laws of inference concerning ‘Bayesian’ hypothesis testing. The right question in these circumstances takes the form “How does the posterior odds ratio (R) compare to the prior odds ratio after the latter has been multiplied by the likelihood ratio made from the data?”. What you’ve correctly derived in b) is the RHS of such an inference – the likelihood ratio times prior odds side – but it’s a likelihood ratio made of ‘L’, not of ‘F’.

¹ posterior: P(I|LFN) / P(~I|LFN) < (≪) prior: P(I|FN) / P(~I|FN) on likelihood ratio constructed from data 'L': P(L|IFN) / P (L|~IFN). Formally correct but of little interest to an inferencer who happens to be a lifeform!
on June 12, 2012 at 11:13 pm | Reply lukebarnes

“Your setup of (3) seems to indicate that you’re well aware that it’s impossible to calculate the actual probability of ‘I’”. What? If by the “actual probability of I” you mean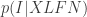 $p(I|XLFN)$ then that’s just

$p(I|XLFN) = \frac{R}{1+R}$ .

(Prove it for yourself).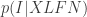 $p(I|XLFN)$ (and hence R) is the right question: what is the probability of the hypothesis I want to test given the evidence that I have? The odds form of Bayes theorem was just more convenient, but the two forms are consistent.

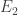I maintain that, when a hypothesis $H$ is being tested by multiple pieces of evidence $E_1$ , $E_2$ , the Bayes formalism gives us some freedom in how we break up the probabilities, as shown in the 2 expressions for R in my previous comment. It is a Bayesian inference on X, L, F and N – all of those pieces of evidence are there. The subsequent manipulations of the expression for R don’t change the fact that the inference is on all of these pieces of evidence, not just one of them.

My final result for R shows that the most important factor is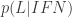 $p(L|IFN)$ (and $p(L|\bar{I}FN)$ ). This doesn’t follow from the fact that I have transformed the problem from a Bayesian inference on one of XLFN to another one. They’re all in there. My conclusion follows from the anthropic principle and the independence of F on I. Other facts about the evidence have shown us that some of XLFN are more important than others. That does not mean that I have made an odds ratio out of some of them while ignoring others.
on June 13, 2012 at 6:21 am | Reply Wolfbone

“If by the “actual probability of I” you mean [...]”

No, of course not. I mean “actual” as in “numerical”. As I said: all we care about and all we can do anyway is see how it /changes/ in the light of some particular evidence about which we can make (semi-)numerical assertions.

“My final result for R shows that the most important factor is [ p(L|IFN) / p(L|~IFN) ]. This doesn’t follow from the fact that I have transformed the problem from a Bayesian inference on one of XLFN to another one.”

All you have shown is that because P(X|LN) = 1, ‘X’ is completely uninformative in the ‘posterior = LR times prior’ inference (3). We learn nothing from ‘X’ about P(I|…)/P(~I|…) so clearly we’d better do a different inference. But then you choose to construct the ‘silly’ one – the one that tells us what happens to our prior estimation of P(I|…) when we learn ‘L’ .

If you had chosen the one you claim to make conclusions about – the one where the fact that we learn is ‘F’ – then by the same argument you use to derive the superfluous P(I|FN)/P(~I|FN) = P(I|N)/P(~I|N), we’d learn nothing about P(I|…) from ‘F’ either.

“It is a Bayesian inference on X, L, F and N – all of those pieces of evidence are there.”

They are there in different roles in different inferences. But since you’re failing to distinguish between the case when a piece of evidence E_i appears in an inference as given fact and the case when it appears (in the likelihood ratio) as the data from which we are, supposedly, actually inferring something, what you’re doing isn’t (a Bayesian) inference.
- on June 13, 2012 at 8:03 pm | Reply Wolfbone
  
  … Perhaps I should point out that it doesn’t make any difference even if we don’t want to view the problem as a number of different inferences: We have (semi-)quantitative information for exactly one of the LR factors in the ‘posterior = product of 3 LRs and prior p(I|N)/p(~I|N) inference’ form (as set out in your June 11, 2012 at 11:13 pm comment) – the LR factor which represents learning ‘L’. It’s still obviously not an inference that shows that “learning ‘F’ has increased the probability that whatever set in place the physics of our universe was not indifferent [...]”. Taking logs yields yet another way to view it – as a sum of the amount of evidence provided by each factor: http://www-biba.inrialpes.fr/Jaynes/cc04q.pdf
on June 15, 2012 at 5:17 am | Reply lukebarnes

What if I concluded: “learning F and L has increased the probability that whatever set in place the physics of our universe was not indifferent …”?

Full marks for referencing Jaynes. Note that the result in equation (4-10) doesn’t depend on which part of the data D we label D1 and which we label D2. We don’t have to make D1 the one we learned first or the most obvious bit or the most important bit.

In my case, D = FL. (We agree – I think – that X is not useful information and N is assumed throughout as background information). So I can call D1 = F and D2 = L, as in the post, if I like.
on June 15, 2012 at 7:06 am | Reply Wolfbone

“Full marks for referencing Jaynes.”

As I do at every opportunity. Hopefully one day we’ll see the back of the appalling, irrational mess that is ‘orhodox inference’.

I think the trouble with “learning F and L” is that it still reduces to and means actually learning something only from ‘L’. ‘F’ contributes zero to the ‘amounts of evidence’ sum.
on June 18, 2012 at 3:22 am | Reply lukebarnes

We can test that by leaving out ‘F’.

$\frac{p(I|XLN)}{p(\bar{I}|XLN)} = \frac{p(X|ILN)}{p(X|\bar{I}LN)} \frac{p(L|IN)}{p(L|\bar{I}N)} \frac{p(I|N)}{p(\bar{I}|N)}$
$= \frac{p(L|IN)}{p(L|\bar{I}N)} \frac{p(I|N)}{p(\bar{I}|N)}$

where the second line follows from the anthropic principle. Now, what is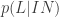 $p(L|IN)$ and $p(L|\bar{I}N)$ ? In the absence of F, we might think that some sort of life is the kind of thing that would happen in any old universe. In particular, we might think of the odds of an indifferently effected universe weren’t too low. 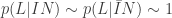So we might conclude (and I think many people before the 1970′s would have concluded) that $p(L|IN) \sim p(L|\bar{I}N) \sim 1$ .

Thus, F is crucial to the argument because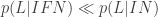 $p(L|IFN) \ll p(L|IN)$ . It is F that makes L a surprising, unlikely fact *given* I. If you like, there is a probabilistic ‘tension’ in the conjunction IFL – each is unlikely given the other two. It is precisely this kind of tension that sends us off to look for other hypotheses. Frank Wilzcek (http://arxiv.org/pdf/hep-ph/0512187v2.pdf) said it well:
“The happy coincidences between life’s requirements and nature’s choices of parameter values might be just a series of flukes, but one could be forgiven for begin- ning to suspect that something deeper is at work. That suspicion is the first deep root of anthropic reasoning.”
on June 18, 2012 at 1:58 pm | Reply Paul Lawrence Hayes

“[...] It is F that makes L a surprising, unlikely fact *given* I.”

In an inferential context in which it’s reasonable to regard ‘L’ as a fact which can be learned and can surprise – it is, yes.
on July 27, 2012 at 10:09 pm | Reply donald

I don’t understand why p(L/IFN) << p(L/IN). Shouldn't it be the other way around? The probability of life in a naturalistic universe is much less (I would guess zero) if the laws aren't life friendly. In the subset of universes where the laws are life friendly then the probability of life is higher.

Incidentally, if I recall correctly Ikeda and Jefferys didn't like to see expressions where the probability of life is calculated. They claim that you have to take L as part of your background information, since we know we exist. But I don't think the rules of math forbid one from doing what they say you shouldn't do.
If you ignore their dictum you can formulate the fine-tuning argument in a very simple way–

P(N/L) / P(not N/L) = ( P(L/N) times P(N) ) / ( P(L/ not N) times P(not N) )

There's no need for the F. The claim that the universe is fine-tuned AND that this was very unlikely to occur in a naturalistic process is equivalent to saying that P(L/N) << 1. The theist would claim that P(L/ not N) is high, presumably because a God would want to make intelligent beings, but that's one of three places where the argument is outside the bounds of what we could know. P(N) and P(not N) are inscrutable–one could throw one's hands up and just guess they are each 1/2. But anyway, it's the ratio of P(L/N) to P(L/not N) that is behind all design arguments. Some, like Behe, argue that given our natural laws, his IC systems couldn't evolve without outside help. Others, like Francis Collins, disagree with Behe about that and think evolution is perfectly possible without God's supernatural interference, but believe that the physical constants themselves had to be designed. So those are just two different ways of arguing P(L/N) is low. It is presupposed that P(L/not N) is high.

Ikeda and Jefferys insist that one shouldn't write expressions like P(L/N), but I can't see why not. We often calculate the probability of events that we already know have happened. If I flip two coins and see that both are heads I already know the result, but I can still calculate the chance that this would have happened given fair coins. Why should the fact that we are calculating the chance of our own existence given certain conditions be any different in principle?

As for what the Ikeda/Jefferys argument does show, I think it is what you say–if we can show that life's existence is consistent with the laws of physics, then that fact by itself increases the probability that naturalism is true.
But if you go on to show (if one can) that the probability of life arising via purely natural processes is low (P(L/N) << 1), then that decreases the chance of naturalism, unless of course one could somehow show that P(L/not N) is even smaller.

I think that by claiming you can't write expressions like P(L/N) and introducing terms like F they've taken an argument whose logic is fairly easy to understand (whether or not it is correct or whether any of the factors can be calculated) and succeeded in making it almost incomprehensible.
on July 27, 2012 at 10:54 pm | Reply lukebarnes

“The probability of life in a naturalistic universe is much less (I would guess zero) if the laws aren’t life friendly”. You’ve missed the difference between my “F” and ikeda/Jeffrey’s “F”. In my terminology, F is *not* “the laws of this universe are life-friendly”.

I’ll read the rest of your post in the morning …
on July 31, 2012 at 3:33 am | Reply donald

Oh, you’re right. Now I’ll have to reread your argument, though not right now.
on November 8, 2012 at 10:25 pm | Reply Libby Anne: Portrait of an atheist feminist | Uncommon Descent

[...] it could only count as evidence against God’s existence. Part 1 of Dr. Barnes’ reply is here; Part 2 is [...]
on December 27, 2012 at 1:01 am | Reply Loftus’ faulty argument for atheism gets an F double minus | Uncommon Descent

[...] evidence against God’s existence. Part 1 of Dr. Barnes’ reply to Ikeda and Jeffery is here; Part 2 is [...]

Comments RSS

	A Fish Called Newton… on “Fundamental Harmony bet…
	Big Blue Bump on Appealing to Authority: A User…
	dougaj4 on Appealing to Authority: A User…
	Zeke on Appealing to Authority: A User…
	Big Blue Bump on Appealing to Authority: A User…

Letters to Nature